بررسی بعضی مباحث ریاضی عمومی 1 و 2 در متلب

[skyzare]

پاسخ : بررسی بعضی مباحث ریاضی عمومی 1 و 2 در متلب

با سلام .

ادامه حل دستگاه های معادلات جبری خطی

منبع :

فصل دوم از معادلات جبر خطی مهندس صبا صدقی زاده استاد دانشگاه خواجه نصیر طوسی

=================================================

حالت m<n : تعداد معادله های دستگاه از تعداد مجهولات کمتر است .


برای حل این گونه دستگاه ها نیز می توان از تابع rref استفاده کرد در صورتی که از روش معکوس کردن قادر به حل دستگاه نیستم زیرا ماتریس ضرایب مربعی نبوده در نتیجه قابل معکوس کردن نیست .

مثال :

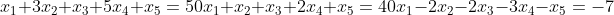
در این مثال تعداد معادلات از تعداد مجهولات کمتر می باشد . ماتریس افزوده دستگاه به فرم زیر می باشد .

حال با نرم افزار متلب فرم سطری پلکانی کاهش یافته آن را به دست می آوریم .

>> A=[1 3 1 5 1 ; 0 1 1 2 1 ; 0 -2 -2 -3 -1 ]

A =

   1   3   1   5   1
   0   1   1   2   1
   0  -2  -2  -3  -1

>> b=[5 ; 4 ; -7 ]

b =

   5
   4
  -7

>> C=[A , b ]

C =

   1   3   1   5   1   5
   0   1   1   2   1   4
   0  -2  -2  -3  -1  -7




>> S=rref(C)

S =

   1   0  -2   0  -1  -6
   0   1   1   0  -1   2
   0   0   0   1   1   1 

بنابراین دستگاه اصلی هم ارز با :

از آنجائیکه تعداد مجهولات بیشتر از تعداد معادلات می باشند ، می توان برخی از مجهولات را بر حسب دیگری به دست آورد . بنابراین دستگاه بی نهایت جواب دارد .

و با توجه به این جواب ها ، متغیرهای x x x مستقل نبوده و وابسته به مقدار x و x هستند

که به x و x متغیرهای آزاد ( Free Variables ) نیز گفته می شود .

با کمی دقت می توان دریافت که متغیر های x x x مربوط به ستون هایی هستند که عناصر محوری در آنها قرار دارند .



تعریف عناصر محوری : Pivot Entry

اولین درایه غیر صفر ( در صورت وجود ) هر سطر ماتریس سطری پلکانی کاهش یافته برابر با یک می باشد . که به آن عنصر محوری گفته می شود

در شکل زیر نمایی از یک ماتریس سطری پلکانی کاهش یافته مشاهده می شود که یک های با پس زمینه سبز رنگ عناصر محوری می باشند .

==============================================

در حالتی که تعداد معادلات بیشتر از مجهولات باشد نیز به همین صورت عمل می شود .

==============================================

**************************

یکشنبه 20 فروردین 91

91/1/20

[skyzare]

تشخیص سازگار یا ناسازگار بودن دستگاه معادلات با تابع rref

با سلام .


عنوان : تشخیص سازگار یا ناسازگار بودن دستگاه معادلات با تابع rref


منبع :

فصل دوم از معادلات جبر خطی مهندس صبا صدقی زاده استاد دانشگاه خواجه نصیر طوسی

=================================================

یکی از کاربردهای دستور rref در تشخیص سازگار یا ناسازگار بودن دستگاه معادلات است . معادلات معرفی شده با ماتریس افزوده [A│b] زمانی سازگار است که در فرم سطری پلکانی کاهش یافته یا فرم سطری پلکانی آن ، سطری به شکل زیر ظاهر نشده باشد .

در غیر این صورت معادله حاصل از سطر مذکور به صورت زیر خواهد آمد :

که برای این معادله راه حلی ندارد و در نتیجه دستگاه معادلات خطی اصلی ناسازگار خواهد بود .


مثال : سازگاری یا ناسازگاری دستگاه زیر را بررسی نمایید .

برای محاسبه دستی باید فرم سطری پلکانی کاهش یافته ماتریس افزوده رو با استفاده از روش حذفی گوس به دست آورد . اگر سطری شرایط ذکر شده در بالا را داشته باشد دستگاه ناسازگار است و هیچ جوابی ندارد .


بررسی با متلب :

>> A=[2 -1 1 0 ;3 1 -1 1 ;1 2 -2 -1 ; 1 1 -1 1 ]

A =

   2  -1   1   0
   3   1  -1   1
   1   2  -2  -1
   1   1  -1   1

>> b=[2 ; 1 ; 4 ; 5 ]

b =

   2
   1
   4
   5

>> C=[A,b]

C =

   2  -1   1   0   2
   3   1  -1   1   1
   1   2  -2  -1   4
   1   1  -1   1   5

>> S=rref(C)

S =

   1   0   0   0   0
   0   1  -1   0   0
   0   0   0   1   0
   0   0   0   0   1 

همان طور که مشاهده می شود اگر بخوایم معادله سطر چهارم ماتریس S را بنویسیم به فرم زیر می شود :

بنابراین دستگاه اصلا جواب ندارد و ناسازگار می باشد .


البته با استفاده از پیدا کردن رتبه ماتریس افزوده و ماتریس ضرایب و مقایسه این دو می توان سازگاری با ناسازگاری دستگاه را تشخیص داد .

****************************

شنبه 26 / 1 / 91

[skyzare]

تشخیص مستقل خطی با وابسته خطی بودن مجموعه ای از بردار ها

با سلام .

عنوان : تشخیص مستقل خطی یا وابسته خطی بودن مجموعه ای از بردار ها با استفاده از تابع rref


منبع :

فصل دوم از معادلات جبر خطی مهندس صبا صدقی زاده استاد دانشگاه خواجه نصیر طوسی

و

فصل سوم ( فضای برداری )آ از معادلات جبر خطی مهندس صبا صدقی زاده استاد دانشگاه خواجه نصیر طوسی

================================================== ====

تعریف مستقل خطی و وابسته خطی :

بردارهای را مستقل خطی ( Linear Independent ) گویند اگر معادله ای به شکل زیر :

که در آنها اسکالرهای ثابتی هستند فقط به ازای شرط

برقرار باشد در غیر این صورت برارهای را وابسته خطی ( Linear Dependent ) گویند

نکته : شرط لازم و کافی برای مستقل خطی بودن بردارهای که هر یک دارای nآ عنصر هستند آن است که دترمینال ماتریس ضرایب n*n مخالف صفر باشد . زیرا در این صورت دستگاه تنها یک جواب دارد و آن هم بردار صفر می باشد بنابراین شرط مستقل خطی برقرار می شود .


در نرم افزار متلب می توان از دستور برای تشخیص استقلال خطی بردارها استفاده نمود. در این جا R فرم سطری پلکانی کاهش یافته و P برداری است که محل عناصر محوری و به عبارتی بردارهای مستقل خطی را نشان می دهد .

================================================== ====

مثال :

استقلال خطی با وابستگی خطی بردارهای زیر را بررسی کنید .

با توجه به تعریف داریم :

با جمع کردن داریم :

دستگاه معادلات و فرم سطری پلکانی کاهش یافته آن به صورت زیر می باشد :

با توجه به محل عناصر محوری ( یک های قرمز رنگ )آ متغیر آزاد است و بقیه متغیر ها را می توان بر حسب این متغیر آزاد نوشت :

هم چنین عناصر محوری نشان می دهند که u1 و u2 مستقل خطی و بردار u3 به آنها وابسته است . پس در مجموع بردارهای u1 u2 u3 وابسته خطی می باشند .

================================================== ====

بررسی با متلب :

در نرم افزار متلب می توان از دستور برای تشخیص استقلال خطی بردارها استفاده کرد . در این جا R فرم سطری پلکانی کاهش یافته و P برداری است که محل عناصر محوری و به عبارتی بردارهای مستقل خطی را نمایش می دهد .

>> u1=[-2;1];
>> u2=[-1;-3];
>> u3=[4;-2];
>> U=[u1 u2 u3];
>> u1

u1 =

  -2
   1

>> u2

u2 =

  -1
  -3

>> u3

u3 =

   4
  -2

>> U

U =

  -2  -1   4
   1  -3  -2

>> [R P]=rref(U)

R =

   1   0  -2
   0   1   0


P =

   1   2

>> Independent_vector=U(:,P)

Independent_vector =

  -2  -1
   1  -3

>> 

****************************

شنبه 26 / 1 / 91

[skyzare]

پاسخ : بررسی بعضی مباحث ریاضی عمومی 1 و 2 در متلب

با سلام .

این هم یه فایل پیرامون همین موضوع . یه فایل زیپ شده هست که هم فایل ورد و هم فایل pdf و هم فونت های استفاده شده رو داره .

بررسی بعضی از مباحث ریاضی در متلب

[elrajabi]

پاسخ : بررسی بعضی مباحث ریاضی عمومی 1 و 2 در متلب

سلام تابع نرم در زبان متلب ب چه صورت باید بنویسیم؟
norm p
فرمولش هم زیگما i از یک تا n . قدر مطلق xi به توان p کلش بروی یک pام
کمکم کنید
اگر بخوام p رو بین 1 تا 2 انتخاب کنم چیکار باید بکنم

[ghanbarri]

پاسخ : بررسی بعضی مباحث ریاضی عمومی 1 و 2 در متلب

سلام.میشه توضیح بدین در حالت فرو معین،منظور از مینیمم کردن نرم چی هست؟و چجوری میتواند این ماتریس را حل کند.
؟